*Likelihood
- Probability density function(PDF)
-- 평균 $\mu_0$, 분산1을 독립 정규분포를 따르는 확률변수 $X_i$의 확률분포함수(확률밀도함수; 연속형변수)
$f(x_i) = \frac{1}{\sqrt{2\pi\cdot 1}}exp\left( -\frac{(x_i-\mu_0)^2}{2\cdot1}\right)$
-$X_1 = x_1, X_2 = x_2, X_3 = x_3$, 3개의 자료가 있을떄, 확류분포 함수 적용
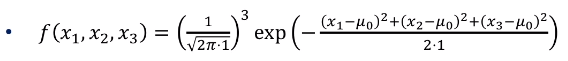
- Likelihood function
-- 동일한 함수이나 $\mu_0$를 변수로 인식
(세미콜론은 주어졌다는 의미)

-- $X_1 = 1, X_2 = 2, X_3 = 3$ 일때

-- 예시 그래프

*무료 그래프 사이트 https://www.desmos.com/calculator
-- 예시그래프를 보면 $\mu_0$ 값이 2일 확률이 가장 높음
-- 가능도 함수를 통해서 모수를 추정하는과정을 나타냄
- Maximum Likelihood Estimator(MLE)
-- 정의: Likelihood를 최대로 만드는 모수의 값

-- 주로 모수에 hat을 붙여 $\left(\hat{\mu_0}\right)$표현
-- Likelihood는 $\mu_0$에 대한 함수이며
$\hat{\mu_0}$=최대값을 가지는 $\mu_0$ -> 극대값 -> Likelihood를 $\mu_0$로 미분해서 0인 값
-- 접선의 기울기가 0이 되는 지점의 모수값이 MLE 이며, 그림1에서는 2이다.
* 미분의 활용 - MLE
- $\mu_0$ MLE 구하기
-- Likelihood 구성

-- 미분하기 용이하도록 log Likeliood 구성
--- 로그를 취하면 복잡한 식이 간단해 질 수 있음(다음과 같이)

-- 미분 실행



-- 미분한 함수가 0 이 되게하는 $\hat{\mu_0}$를 구해냄

-- 결론: $\hat{\mu_0} = \bar{X}$, MLE 가 모수평균와 같다.
-- 미분을 하는 이유는 MLE를 구하기 위함이며 MLE는 모수 추정을 위한 likelihood중 최대값
- $\sigma^2$ MLE 구하기
-- Likelihood 구성, $\lambda = \sigma^2$

-- 미분하기 용이하도록 log Likelihood 구성

-- 미분실행



-- 미분한 함수가 0이 되게하는 $\hat{\lambda}$를 구해냄
